Sponsor:
Air Force Office of Scientific Research (AFOSR), under the Department of Defense (DOD), under award number FA9550-12-1-0458; and National Institute of Standards and Technology (NIST), under Award No. 70NANB14H012.
Project Team Members:
Northwestern University
University of Michigan-Ann Arbor
Georgia Institute of Technology
Materials Optimization Design with Pruned-Search
Overview
This project is kind of special. You know how in scientific research a lot of findings are accidental? The outcome of this project contributes to another evidence of this saying. We started out with a goal to solve an optimization design problem in materials engineering: suppose you are given a set of design variables and you are allowed to change their values semi-freely, that is, under some constraints. For example, each variable can only take values between 0 and 1, and the sum of all variable values equals 1. And what you want is to set them all at some legitimate values (which results in a legitimate design) so that the property you are designing reaches the optimum.
Natually we turn to optimization tools to solve this problem. All we need is an objective function that takes in design variable values and spits out objective values, and the set of constraints to set the boundary of legitimacy. There is a large body of literature for optimization methods ready for you to explore. The story could end here with picking up the right optimization tool that conducts the many searches within our design space to hopefully find the best value. Maybe devlopping some tricks here and there to avoid local optima, as the objective function in materials design is never convex.
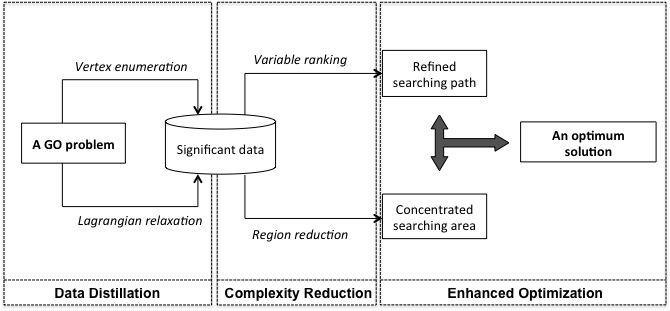
Method
We meant to make search better. But how? The idea is to have the search force focused in a more promising path and prune (hence the name) the irrelevant effort. The validity of this heuristic is rooted in two assumptions. Fristly, we assume the desired function value depends only on a reduced, albeit unknown, set of variables. Secondly, we assume that the impact of each variable to the search value is different. Hence, there exists an optimal order in terms of searching priority.
Suppose we buy these stated assumptions. The next questions to ask is how to obtain an optimal search path, and at the same time, reduce the viable search region of each variable so that it is faster. We turn to data science to draw insights. For that a representative set of data needs to be collected. We call that process data distillation (see [1]). Afterwards we perform complexity reduction on two branches, in parallel: one creates an ordered list of variables based on their impact towards the function, and the other reduces of the feasible region for each variable. The former is achieved through feature selection methods where a ranking is guaranteed. The latter is realized through examining a rule-based classifier and looking for the critical thresholds.
After the above steps, meta-heuristics about searching are obtained. Optimization becomes a much promising endeavor now that the search space is pruned. We then employ a simple line search algorithm that takes a prefixed searching order, and replace the original constraints with the pruned ones.
Results
The first set of results is presented in [2], where we apply the strategy in five materials property optimization problems. The additional difficulty in this problem setting is that there could be multiple answers that lead to the same local optimum. It turns out our method not only helps reducing the search complexity (make it faster), but also is able to identify multiple optimal solutions effectively.
Then we went further to see if this developed framework is applicable to general optimization problems (non-materials science related). A number of such problems from literature are studied in [1], and the conclusion holds. Both the searching speed and result accuracy have been improved.
Software Download
Pruned search software can be downloaded here. It is a general optimization package that performs search space reduction given an objective function and mathematical constraints, although the example demo provided is related to a certain materials property.Publications
- [1] Ruoqian Liu, Ankit Agrawal, Wei-keng Liao, Alok Choudhary, and Zhengzhang Chen. Pruned Search: A Machine Learning Based Meta-Heuristic Approach for Constrained Continuous Optimization. In the Eighth International Conference on Contemporary Computing (IC3), August 2015. (pdf)
- [2] Ruoqian Liu, Abhishek Kumar, Zhengzhang Chen, Ankit Agrawal, Veera Sundararaghavan, and Alok Choudhary. A predictive machine learning approach for microstructure optimization and materials design. Scientific Reports, 5:11551, Macmillan Publishers Limited SN, June 2015. (pdf)
- [3] Ruoqian Liu, and Ankit Agrawal, Wei-keng Liao, and Alok Choudhary. Search Space Preprocessing in Solving Complex Optimization Problems. In the Workshop on Complexity for Big Data held in conjunction with the IEEE International Conference on Big Data, October 2014. (pdf)
Acknowledgements
This work is supported by AFOSR (Air Force Office of Scientific Research), Department of Defense (DOD) under Award No. FA9550-12-1-0458; and by National Institute of Standards and Technology (NIST), under Award No. 70NANB14H012.




