Sponsor:

Advanced Scientific Computing Research (ASCR) under the U.S. Department of Energy Office of Science (Office of Science)

Project Team Members:

Northwestern University

• Alok Choudhary
• Wei-keng Liao
• Kui Gao
• Saba Sehrish
• Chen Jin
• William Hendrix
• Seung Woo Son

The HDF Group

• Quincey Koziol
• Gerd Herber

Argonne National Laboratory

• Rob Ross
• Rob Latham
• Tim Tautges
• Venkat Vishwanath

North Carolina State University

• Nagiza Samatova
• Sriram Lakshminarasimhan

---

---

Damsel Usecase - a simple 2D

Just to get the ball rolling on these use cases, here is a simple example. Let us represent a 2D array in the proposed data model.

Description:

Consider a 2D (N by M) array of double-precision floating point values. For the sake of this discussion we will assume the application has cell-centered data. This 2D array represents surface barometric pressure over some land area.

Requirements

Fairly straightforward requirements. This use case is perhaps the simplest we can imagine. Damsel will represent far more complicated data models, but this simple case should not be high-overhead.

Narrative

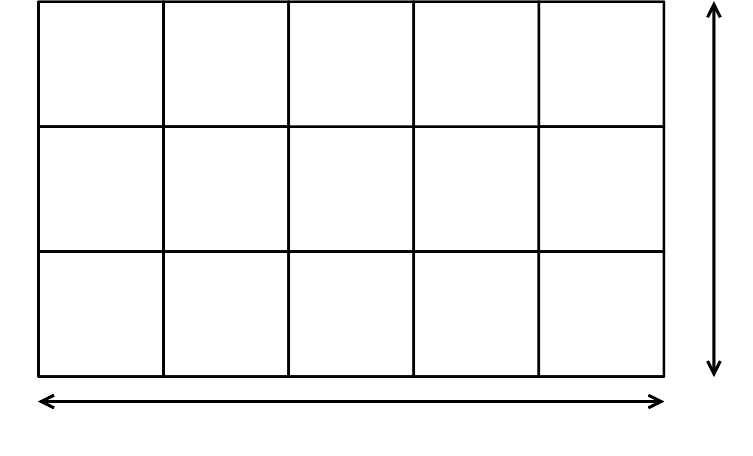
What HDF5 and pnetcdf think of as a 2d array, our data model sees as a 2d structured mesh. Our N by M array will be a collection of N*M entities arranged in such a mesh. In this figure the entities carry an identifier.

The description in terms of the data model:

1. Structured vertex block: x0, y0 = (0, 0); dx, dy = (1.0, 1.0); IMIN/IMAX = (0, 5); JMIN/JMAX = (0, 3); --> block b1, start handle-- --h1
2. Structured quad block: uses b1 --> block b2, start handle-- --h2
3. Units: create units "entry" (kg/1/0, m/0/1, s/0/2) -->-- --units handle h3
4. Tag: name "surface_barometric_pressure"; size type = fixed; size sizeof(double); data type = double; default value = -1.0; storage type = dense; associated with units handle h3 --> tag handle h4
5. Tag values: input double* pointing to (IMAX-IMIN)(JMAX-JMIN) = 15 pressure values, assigned to tag h4 on entities in b2 -->-- --assigned value for tag h4 on quads-- --[h2, h2+15)

Responses to questions

Once the polygons have been defined, we need to describe how those polygons are connected to each other. In the case of a structured mesh, connectivity is implied by associating structured vertex block b1 to quad block b2. Connectivity means the vertices defining each quad; adjacency means quad h2+1 is adjacent to quad h2+2 through two of its vertices, h1+2, h1+2+(IMAX-IMIN+1)=h1+8.

• Entity Handle: in this simple example each polygon has an integer identifier
• We should start thinking of these as handles, at least initially. Maybe eventually they get implemented as integers, but we want to let the implementations decide that. In MOAB, we gain a lot by embedding the entity type (vertex, tri, etc.) as the high 4 bits of a handle, while preserving the ability to increment, put in ranges, etc.
• High-Order entity: In this simple example I don't think there are any high-order entities. The corners sufficiently bound the array/mesh
• Correct.
• Entity Set: This entity is part of the root set and has no parent or child entities
• Correct. Though, I'm on the fence on whether each block should be assigned its set (would allow us to embed IMAX/IMIN and dx/dy as tags on the set, which would by definition get preserved with the mesh, with no special handling as "parametric extents of a block"; that's what MOAB's structured mesh interface does).
• Tags: is this the actual data of the application array? When I hear 'tag' I think 'annotations' and other optional data.
• Yes, the actual data, though tags can also be used for the kind of optional annotations you're thinking of too. I usually distinguish the two on storage type, with field-type data put on dense tags and annotation-type data on sparse tags.
• Block: this entity consists of handles 0-15, which will be bound into a block.
• You probably mean 0-14 here; to be less specific about how handles are implemented, I represent these as [h2,h2+15). Note the h2+15 is significant here, implying that though we're allowing implementations to use whatever type they want, we do require that that type have an increment operator.
• Structured Mesh Block: Here we can use the equal spacing of the vertices of the 2d array to express the vertices algorithmically as such: (0,0) specifies the origin. Our delta in x and y is 1 "unit"
• Yes.
• where would that be defined?
• In the input to creating the structured vertex block. Note, I've written it as part of the block creation, but we could make that a separate operation that could happen later.
• So our delta tuple is (1,1). where are the maximum in x and y specified?
• The maximum in x and y are implied by the origin at (0,0), the dx,dy of (1,1), and the IMIN/IMAX, JMIN/JMAX specified earlier.
• Dimension: We have an X and Y dimension (in the figure, 5 and 3). Also, our mesh and our array have the same discretization.
• it is asserted that in this case we don't need a dimension, since the array is associated with a structured mesh block. In other words, is there any other reason why we need this dimension, other than to specify how many values for this field that we expect? I've basically replaced the dimension you used before with the parametric description of a structured vertex block. Stated another way, because we've defined blocks b1 (structured vertices) and b2 (structured quads), there's no need for 4 dimensions (you'd need the extra 2 if you also wanted to write vertex-centered data).
• Space: our space, named "2d array" groups the X and Y dimensions defined above.
• Again, no need for this; replaced with blocks b1, b2 and associated parameter extents.

EECS Home | McCormick Home | Northwestern Home | Calendar: Plan-It Purple © 2011 Robert R. McCormick School of Engineering and Applied Science, Northwestern University "Tech": 2145 Sheridan Rd, Tech L359, Evanston IL 60208-3118  |  Phone: (847) 491-5410  |  Fax: (847) 491-4455 "Ford": 2133 Sheridan Rd, Ford Building, Rm 3-320, Evanston, IL 60208  |  Fax: (847) 491-5258 Email Director Last Updated: $LastChangedDate: 2014-09-17 14:51:09 -0500 (Wed, 17 Sep 2014) $